Following the very popular post of last week on Games with Fancy Names, today I have a new game. A biased coin will be tossed 1807 times. The coin bias is only 51.96%, meaning that on the average, heads will come up 51.96% of the time. You win $67.28 each time the outcome is a head and you pay $60.16 if it is a tail. No commissions paid and you do not have to worry about consecutive losers that may wipe out your starting bankroll. Does this game sound like something familiar?
Notice that this time around it is obvious that this is a profitable game because the average win is larger than the average loss. In the case of GLD the average win was less than the average loss and it was not immediately evident whether that was a profitable game until someone actually calculated the expected value.
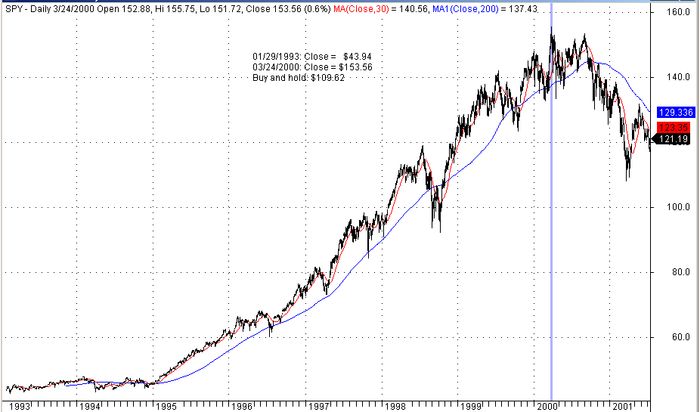
Welcome to SPY, the popular ETF, in the period from 01/29/1993 to 03/24/2000, when it made an all time intraday high of $155.75:
In this period there was a spectacular rally with a buy and hold gain of $109.62 per share excluding paid dividends.
The analogous game in the case of SPY is the following: Each day at the close you purchase 100 shares and exit at the close of the next day. No commissions apply. Each time there is a positive close (heads) you win $67.28 on the average and each time there is a negative close you lose $60.16 on the average. The game has of course positive expectation and it is profitable over the period considered. The statistics are as follows:
Total number of days (tosses): 1807
Number of heads (positive close): 939
Number of tails (negative close): 868
Bias (No of heads/No of tosses) = 939/1807 = 0.5196 or 51.96%
Average winner per share: $0.6728
Average loser per share: $0.6016
The expectation of this game is given by the following formula:
EV = win rate * avg. winner – (1-win rate) * avg. loser
= 0.5196 * $0.6728 – (1 – 0.5196) * $0.6016
= $0.06058
EV x 1807 = $0.06058 * 1807 = $109.62
which is equal to the buy and hold profit per SPY share over the period considered.
Notice that the expectation for SPY of $0.06058 per share traded is approximately equal to the expectation calculated for GLD in the previous game and equal to $0.0684.
The lesson and key point is not that the game just described was profitable but that the spectacular trend in SPY during the period under investigation was achieved by a very small winning bias, even smaller than in the case of GLD. Huge profits can be accumulated slowly via a game that offers a very small bias and small positive expectation, even if the ratio of average win to average loss is slightly greater than one. Any trader or investor who can spot such games on time can make huge profits over a period of 2 – 4 years. Of course, there are issues of commission cost and risk of ruin due to a streak of consecutive losses that may exceed initial bankroll but these will be topics of another post.
These are the games people play and they give them fancy names like SPY.
Have a good trading day!
Charting program: Amibroker (Charts created with AmiBroker – advanced charting and technical analysis software. http://www.amibroker.com/”)
Disclaimer:The author is not a financial advisor and does not recommend the purchase of any security or advise on the suitability of any trade or investment in any timeframe. ETF, stock, futures, forex and options trading and investing involves substantial financial risks and can result in total loss of capital. If investment or other professional advice is required, a licensed professional should be consulted.