In a recent post I demonstrated that frequent short-term and intraday forex trading are negative-sum games when spread is included. In the case of intraday forex trading, this is true even at low spreads. Here I demonstrate that E-mini intraday trading is a negative-sum game in the longer term even when commission is $1 per side.
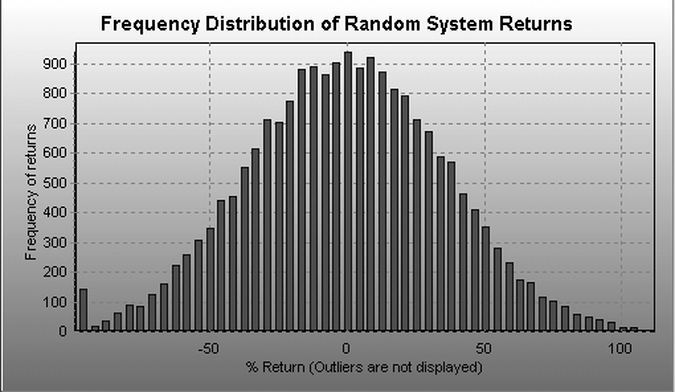
The graph below shows the distribution of net returns (100xprofit/initial equity) of 20,000 random E-mini trading systems on 15-minute data spanning a period of 8 years, from 01/2001 to 12/2008. The starting capital is $100,000 per contract traded. Note that it does not even make sense to consider lower capitalization levels because the results will be a lot worse than those shown below. No commission and slippage is included in the simulation.
The distribution is nearly normal with a mean of -0.14% and standard deviation equal to 35.83%. The kurtosis is -0.086 and the skewness is 0.0018. The minimum return is -97.97% and the maximum is 132.18%. Note that returns below -100% are not allowed because when the equity drops below a margin requirement of $3,500 trading stops.
According to the distribution shown above, 0.65% of the 20,000 systems were stopped and 49.81% produced a positive return. This may sound promising at first glance but this is what happens when $1 of commission and slippage is added to each transaction:
Not even one system out of the 20,000 remains profitable after the introduction of a relatively small slippage and commission. Given that just the exchange fee for trading this contract is about $1.14 per side for retail, you can understand why some claim that 99% of intraday traders are losers. Actually, the winners are extraordinarily lucky but if they stay long enough in the game they lose everything because, due to its nature and by design, this is a negative-sum game.
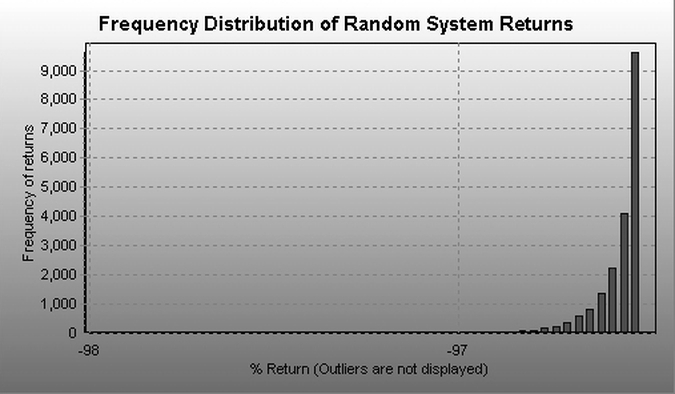
For the second distribution, the mean is -96% , i.e. we are talking about 100% ruin of all systems in the longer term.
Someone could argue that random systems are not intelligent enough to capture returns. But how is “intelligence” defined? We know that at the quantum level the world is random, as particles appear suddenly and vanish, in some cases without any apparent reason. However, the result is what we see, the presumably deterministic world. I could reverse the argument and claim that some seemingly “intelligent” system is actually a random one that camouflages itself as intelligent inside the jungle of random data and achieves that through curve-fitting. We can argue for years or even decades and never reach a conclusion because the ultimate nature of reality is unknown to us.
Related post
Disclosure: no relevant positions.
Disclaimer
