The S&P 500 is an intelligent trading strategy and a popular benchmark. I show below that the probability of obtaining the mean return of the S&P 500 by chance is extremely low.
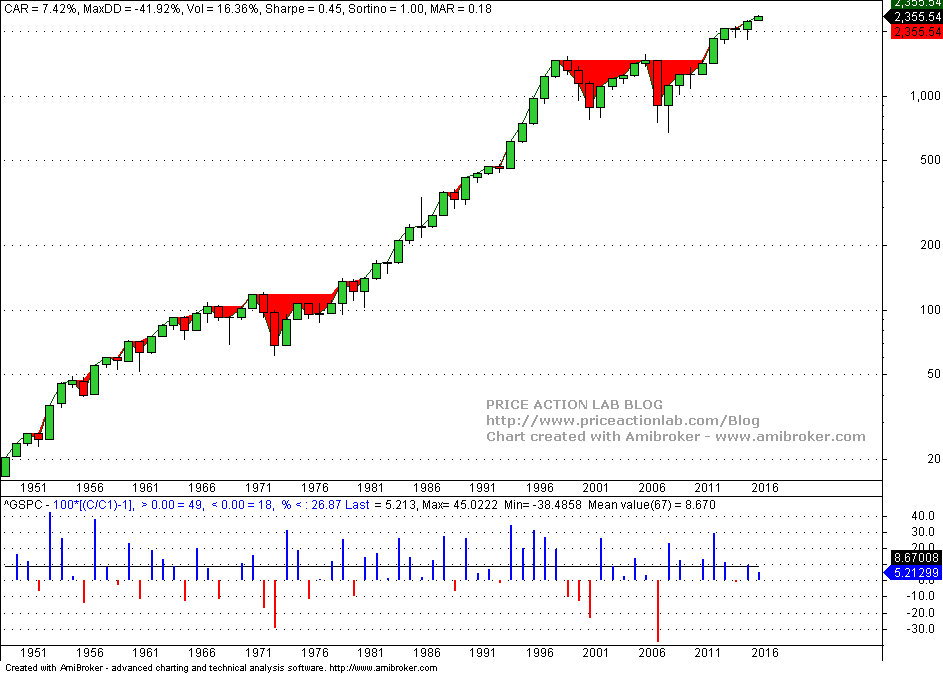
Below is a yearly chart of S&P 500 since 1950 with key statistics:
If we assume an approximately normal distribution and independent returns (see below), the t-statistic for testing the null hypothesis that the average return, excluding 2017, is drawn from a population of zero mean, is given by:
t-statistic = (mean return/standard deviation) × sqrt(number of years)
= (8.722/16.735) × sqrt(66) = 4.2342
For a one-tailed hypothesis, the corresponding p-value is 3.3E-05. Therefore, the probability that the mean return of the sample is drawn from a population with zero mean is 0.0033% and the null hypothesis is rejected.
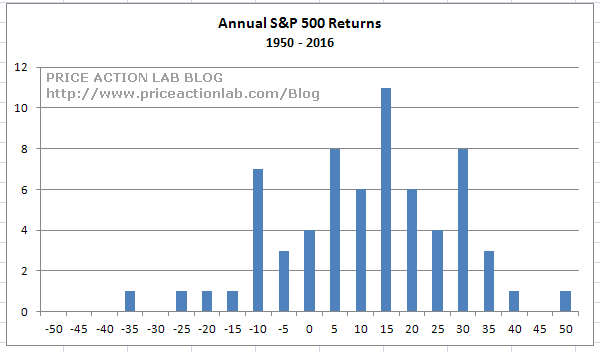
However, the distribution of annual returns is not exactly normal. Below is how it looks like:
Note that the Shapiro-Wilk test yields a p-value of 0.580997 and the null hypothesis of normality cannot be rejected. However, in case we are suspicious of the test results, we can perform a bootstrap of annual returns to get a sampling distribution. This distribution will be normal since we have more than 30 data points (years.) Below is the resulting sampling distribution after 500000 samples.
This is a normal distribution as expected with o mean (centered by design) and standard deviation of 2.01635, close to the expected 2.05996 (standard deviation of original sample divided by square root of sample size.) Kurtosis is 0.01095.
The p-value based on a mean return of 8.722 is 2E-06, or 0.0002%. Then, the null hypothesis can be rejected and we can conclude that the annual returns of the S&P 500 (before dividends) were generated by some process with a positive bias. Actually, this is evident in this case from just looking at the chart. In other cases, it is not clear from charts. However, note that all hypothesis tests are conditioned on past data. It is possible that at some point the process that generates the S&P 500 annual returns will lose its positive bias. This is the real risk for longer-term passive investors.
Not many strategies can beat the S&P 500 strategy
The S&P 500 is a trading strategy although it is commonly referred to as an index. It is a good strategy, as I showed with basic statistics, maybe because too many people try to outperform it and this creates winners and losers. Since profits of market participants have a Pareto-like distribution, a small percentage of players realize the bulk of the profits and that makes the index performance hard to beat. The S&P 500 index is an intelligent trading strategy despite any bear markets. In order to beat it, one must be more intelligent than the collective wisdom that determines its path.
Charting and backtesting program: Amibroker
If you found this article interesting, you may follow this blog via push notifications, RSS or Email, or in Twitter