A momentum crash occurred on Monday, November 9, 2020, with some financial sites reporting a “one in a lifetime event” with nearly 0 probability. Bloomberg called it “an event that never could happen.” However, the truth is that these events have much higher chances according to probability and statistics. Here is why.
Bloomberg wrote:
… the crash in the momentum factor was so rare that writing out the chances of occurrence on any given day required a 16-digit number — followed by 63 zeroes.
However, the above calculation of chances of occurrence rests on the assumption of a normal distribution of returns. A few things to start with:
- Most momentum factor samples have limited history and are not sufficient to assume any distribution at all.
- Equity returns are not normal and actually far from that. Extreme tail events have much higher probability to occur.
- The realization of an extreme event such as the one that occurred on Monday, November 9, 2020, is actually a confirmation that the distribution is not normal.
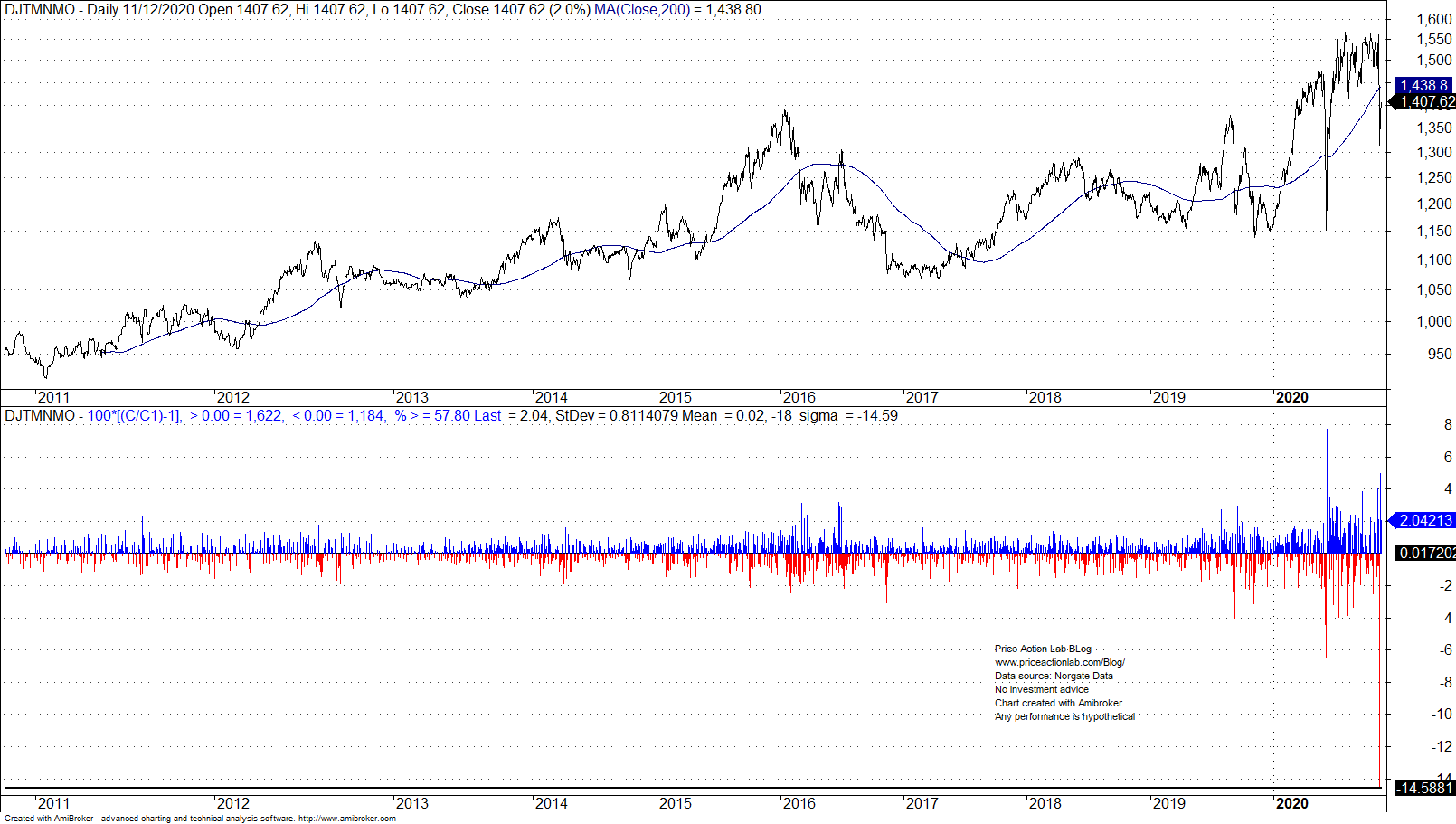
Below is a chart of Dow Jones U.S. Thematic Market Neutral Momentum Index and its daily returns plot, from inception to November 12, 2020.
A -14.6% drop on Monday, November 9, 2020, was around -18 sigma away from the mean of the available sample.
Notice the emphasis above: “of the available sample.” One can actually say that the drop was -18 sigma away the sample mean but must stop there and not try to make any inference about the probability of this drop.
Notice again the last emphasis in the above sentence. Inferences assume knowledge of the distribution. Many made the mistake to call this an extremely rare event. If we assume a normal distribution, the probability of this event is around 7-70, or for all practical purposes 0.
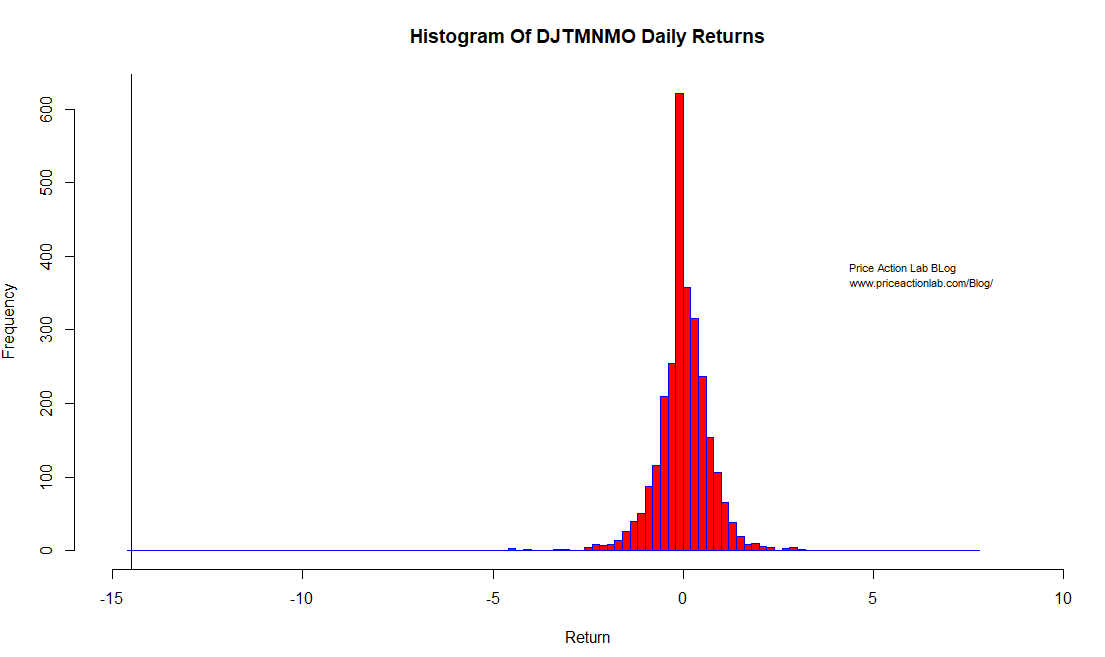
Below are the summary statistics of the daily returns in above chart:
This huge kurtosis points to some fat-tailed distribution shown below:
The vertical black line on the left shows the left tail even of -14.5% for a day.
Below is the skewness-kurtosis plot.
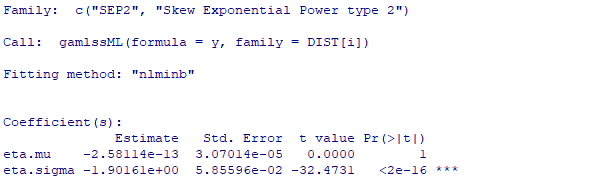
The kurtosis and square of skewness of the distribution suggest fatter tails than log-normal. Next, we fit relevant parametric distributions to get a suggestion about the one that is an “optimal fit” according to generalized Akaike information criterion.
The suggestion is for a “Skew Exponential Power type 2” distribution.
So what does this mean? Roughly, it means that if the distribution is not normal, which we know it is not due to the fact that we observed a large tail event, then the probability of an extreme event such as that observed Monday, November 9, 2020, is not 0% but instead way higher. How much higher is it?
Again, we do not know the exact distribution to infer that. But it could be anywhere from 0.001% to even 0.01% but is not 0% and this was not “a one in a lifetime event.” It will probably occur again and with higher frequency than expected by normal distribution analysis. Risk managers should be aware of these risks and size positions so that such one-day events do not cause uncle point.
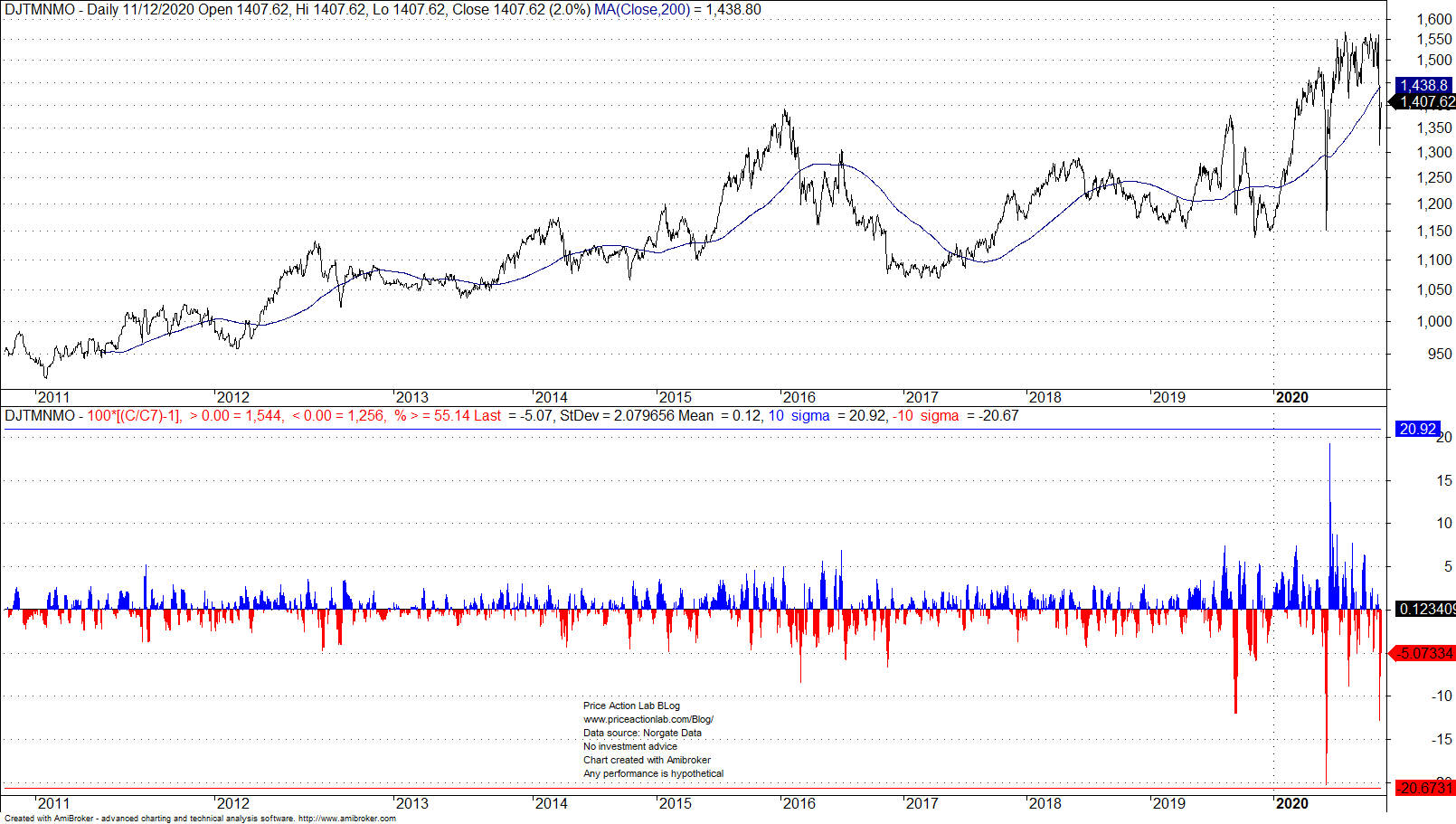
More importantly, people appear infatuated with one-day events but uncle point may occur in the course of a few days. For example, on June 8, 2020, the 7-day return of the same momentum index was -20%, or about -10 sigma of the sample, as shown below. Few spoke about this in financial media.
Although one-day tail events are serious due to liquidation risks, accumulated losses affect risk management and must be also taken into account. It is an irony to survive from one-day loss but then hit uncle point due to a 7-day event.
We expect more tail events in the future in all markets as trading has become more algo-driven and that can affect at certain times the speed and magnitude of daily returns in both directions.
Charting and backtesting program: Amibroker
Data provider: Norgate Data
If you found this article interesting, you may follow this blog via push notifications, RSS or Email, or in Twitter