Backtest results can fool market timers due to randomness and underestimating trading friction. An example is the lumber/gold ratio strategy where there is no alpha but also significant underperformance when compared to buy and hold and simpler alternatives. Journals and financial media should require researchers to account for trading friction effects in their backtests.
In my book Fooled by Technical Analysis: The perils of charting, backtesting and data-mining I argue trading strategy developers should concentrate on determining whether some strategy they have discovered is actually random and not on its assumed merits. Claiming a strategy is good because in a backtest it generates some alpha or higher risk-adjusted returns could be irrelevant. Strategies that appear to have performed well in backtests may be random, or not relevant, due to, among other things:
- Data-mining bias: After many trials a good strategy is selected from a group of failed strategies.
- Lack of accounting for trading friction effects: commission and slippage.
- Not considering a simpler but more effective alternative with fewer transactions.
Unfortunately, in the financial blogosphere, the rate of generation of random strategies for timing the markets or for asset allocation (strategic or tactical) is steadily increasing and few are willing to challenge them because, after all, counter-parties that fail provide profits; there is no incentive to correct mistakes. On the contrary, some of those who understand the subject in depth may even applaud such efforts for the following reason, among others:
An edge maintains its robustness when the number of market participants who execute random strategies increases.
The case of the lumber/gold ratio strategy
Last week, a reader of my blog contacted me and asked me if I could backtest the following strategy:
If lumber is outperforming gold based on 13-week rate-of-change, then invest in stocks.
If lumber is underperforming gold based on 13-week rate-of-change, then invest in short duration bonds.
My blog reader mentioned that there have been claims of superior risk-adjusted returns for this strategy as compared to S&P 500 total return.
I do not recall to have ever seen this strategy before and even if I have, I probably immediately discounted it as random. The reason is simple and backtests are not even necessary; bonds have been on an uptrend since 1990 and even random rebalancing had high chances of generating superior risk-adjusted returns. The annualized volatility of 3 – 5 year U.S. Treasury total return since 1990 is less than 3.5% versus about 18% for S&P 500 total return. Sharpe is bound to increase for most random asset allocation schemes that switch from stocks to bonds. But what happens after we include commissions? According to my blog reader the strategy performance based on the lumber/gold ration he asked me to backtest did not include any commission. This immediately offered a hint about it being random.
Rebalancing a stocks/bonds portfolio based on a random ratio
Before we backtest the strategy based on the lumber/gold ratio, we could try to see what happens if we use a random ratio.
We consider two independent random variables, X1 and X2, uniformly distributed in [0,1]. Every week we sample the uniform distributions and obtain the values for the random variables. Then, the strategy is as follows:
If X1 is greater than X2, then stay invested in stocks.
If X2 is greater than X1, then stay invested in short duration bonds.
For the assets of the portfolio, I use S&P 500 total return ($SPXTR) and 3-5 U.S. Treasury total return ($SPBDU5ST) daily series provided by Norgate Data and then compress to weekly timeframe in the backtester. I highly recommend this end-of-day data service because it takes backtesting to another higher level due to among other things availability of delistings for major stock indexes. (I do not have a referral arrangement with the company.)

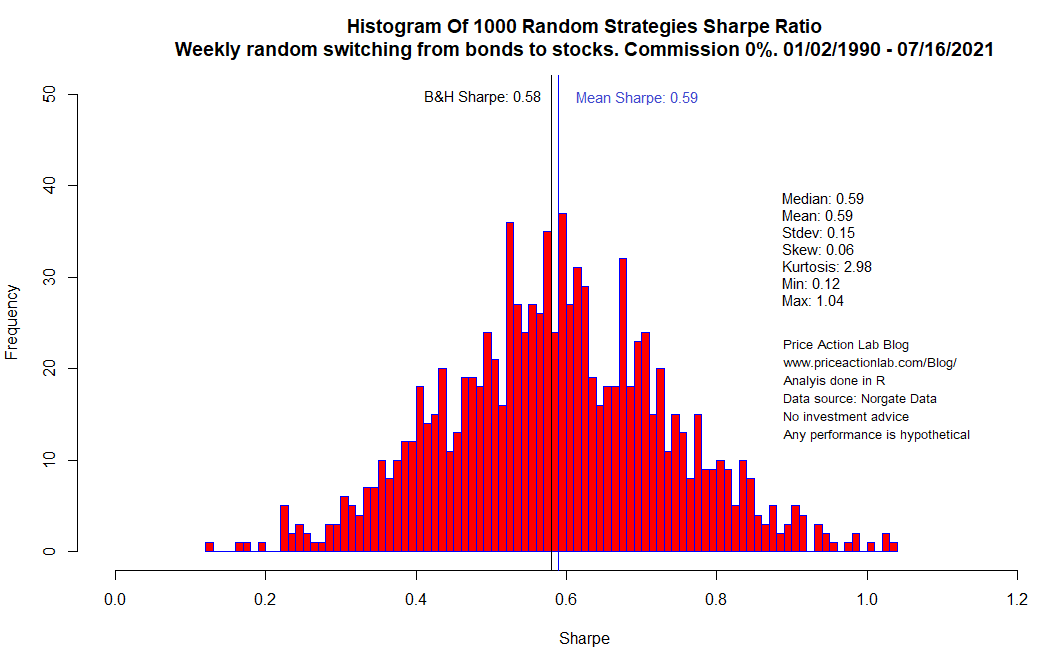
Case 1. No commissions
Below is the histogram of Sharpe ratio.
Mean and median Sharpe are 0.59. About half of the random strategies outperform S&P 500 total return Sharpe at 0.58 and a few strategies have Sharpe above 0.90 due to luck.
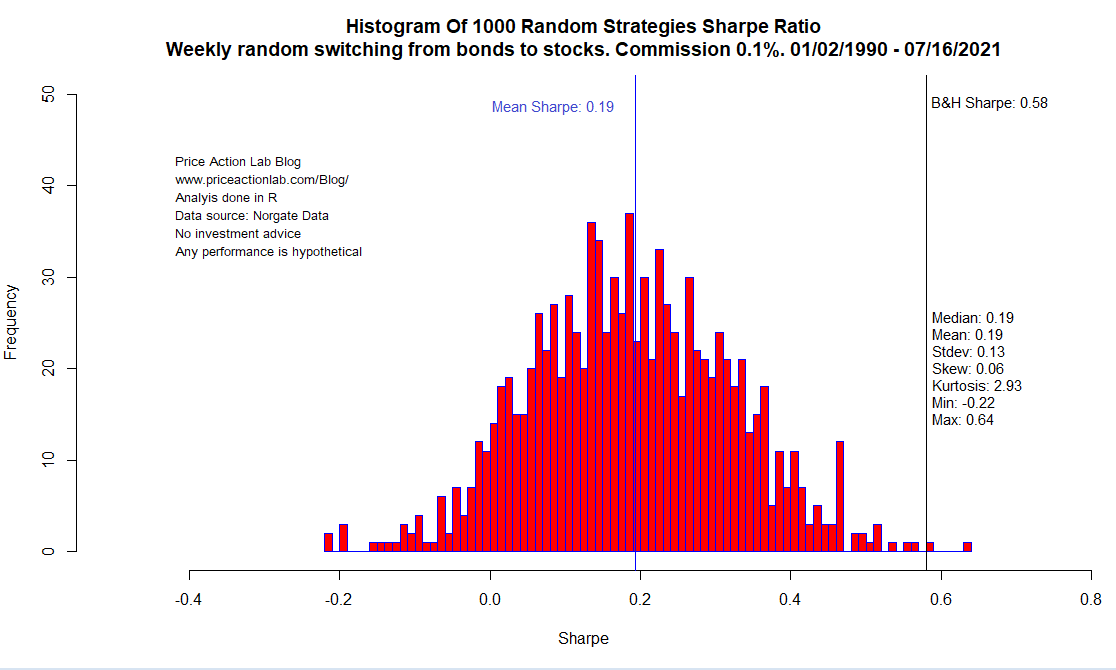
Case 1. 0.1% commission and slippage
Edit 07/24/2021: Someone claimed 0.1% commission and slippage is too high. I agree maybe for the last 10 years but for the 90s it is probably a reasonable number. Regardless, for those who disagree with the number for commission and slippage they should focus on results without it.
I set commission and slippage at 0.1% per trade and repeated the simulation. Below are the results.
Only two strategies outperform buy and hold on a risk-adjusted basis (Sharpe of 0.58) after the introduction of 0.1% commission and slippage. Some strategies have even negative Sharpe. Mean Sharpe collapsed to 0.19 after 0.1% commission was applied versus 0.59 with 0% commission.
These results should ring a bell about using frequent rebalancing with random ratios like lumber/gold. Chances of beating buy and hold are slim when trading friction is taken into account with naïve strategies.
Next, I backtest the lumber/gold strategy and compare to other simpler strategies.
Comparing lumber/gold strategy to two strategies and buy and hold
The other two strategies are as follows:
Strategy 1: Rotation based on 52-week rate-of-change of the assets
If S&P 500 total return is outperforming 3-5 U.S. Treasury total return based on 52-week rate-of-change, then invest in the former.
If S&P 500 total return is underperforming 3-5 U.S. Treasury total return based on 52-week rate-of-change, then invest in the latter.
Strategy 2: Long only price series momentum
Long-only S&P 500 total return if price is above the 12-month moving average.
Exit if price is below the 12-monmth moving average.
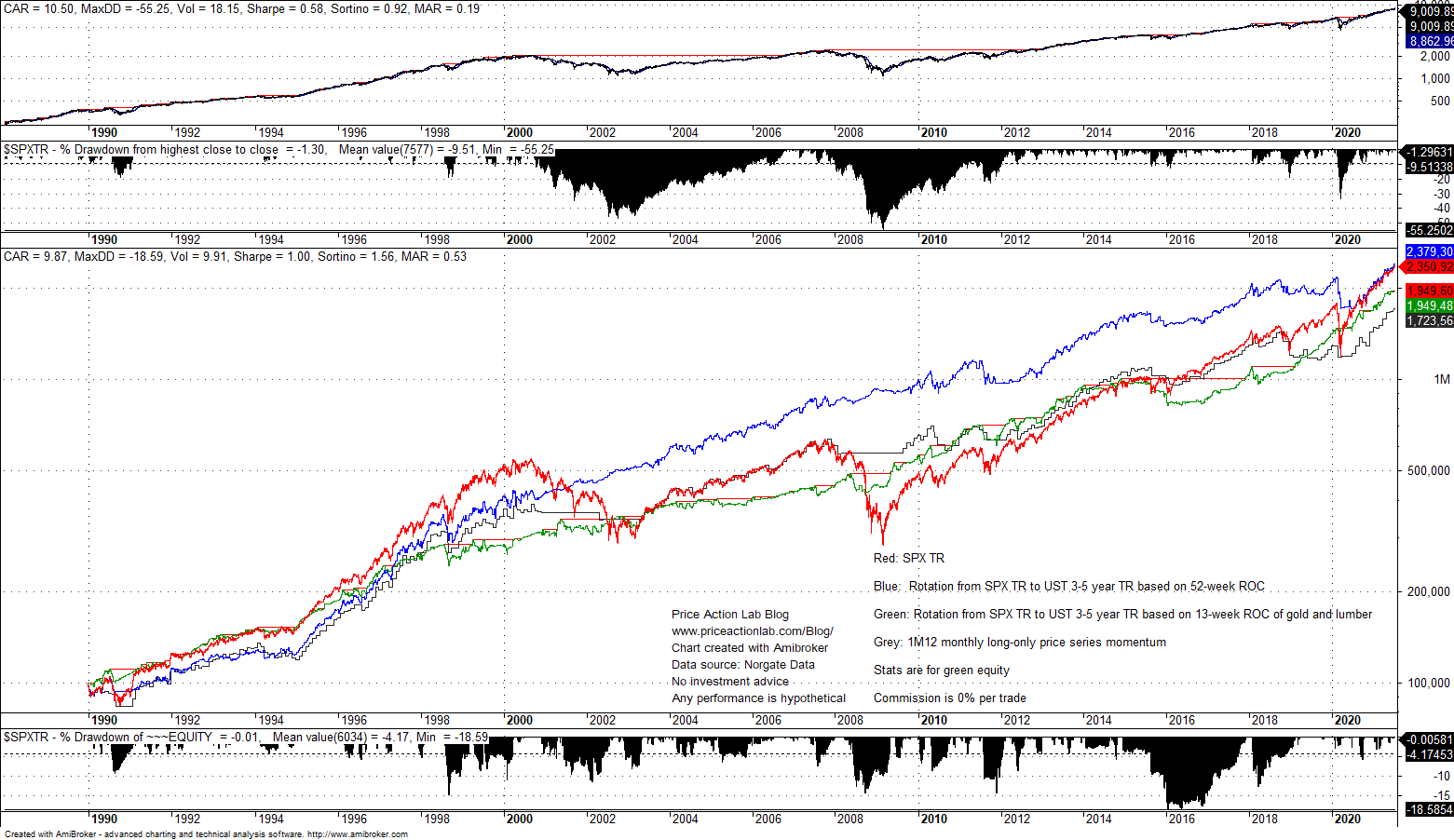
Case 1. No commission
- Blue equity line: Rotation based on 52-week Rate-of-change
- Grey equity line: 12-month S&P 500 total return price series momentum
- Red equity line: S&P 500 total return buy and hold
- Green equity line: Lumber/gold strategy based on 13-week rate-of-change
The statistics on the equity chart are for green equity line and on the first chart the statistics are for S&P 500 total return buy and hold.
It may be seen that although the lumber/gold strategy has Sharpe of 1 and outperforms buy and hold Sharpe of 0.58, it underperforms the simpler alternative based on rotation (blue equity line). In fact, the simple rotation has outperformed the lumber/gold strategy since about 1997 and buy and hold since about 2001. Price series momentum (grey equity lines) has outperformed the lumber/gold strategy from about 1998 to about 2019.
Edit 07/25/2021: Added performance table.
Below is how the four strategies compare. No commission and slippage.
| LUMBER/GOLD | ROTATION | MOMENTUM | BUY & HOLD | |
| CAGR | 9.9% | 10.6% | 9.5% | 10.5% |
| MDD | -18.6% | -21.6% | -18.1% | -55.3% |
| SHARPE | 1.00 | 0.88 | 0.85 | 0.58 |
| WIN% | 68.7% | 69.8% | 52.6% | – |
| TRADES | 195 | 106 | 19 | – |
It is clear that momentum offers a simpler alternative at significantly lower number of transaction. Essentially, exiting stocks completely may be viewed as an equivalent long position in a less risky asset, in this case cash.
Case 2. 0.1% commission and slippage
Next, I apply 0.1% commission and slippage cost to the strategies. Below are the results.
Based on total return, the lumber/gold strategy (green equity line) underperforms all strategies and buy and hold for nearly the full backtest period. In fact, no strategy outperforms buy and hold based on total return performance. However, the simple rotation, or even price series momentum, seem better alternatives to the lumber/gold strategy. Rotation is not affected as much by commissions as the lumber/gold strategy due to a longer rebalancing lookback period of 52 weeks versus 13 weeks.
Underperformance of the lumber/gold strategy of 200 basis point per annum as compared to buying and holding for a period of 31 years results in total return collapsing 43%. It could be argued that 20% maximum drawdown is tolerable versus 55.3% drawdown, as in case of buying and holding, but this is related to risk aversion profile. Regardless, the simple alternative based on rotation has 22.4% maximum drawdown but 130 basis points higher annualized return. This strategy has outperformed buy and hold total return from about 2003 to about 2020 while risk-adjusted returns are superior.
Below is how the four strategies compare with 0.1% commission and slippage.
| LUMBER/GOLD | ROTATION | MOMENTUM | BUY & HOLD | |
| CAGR | 8.5% | 9.8% | 9.3% | 10.5% |
| MDD | -20.5% | -22.4% | -19.4% | -55.3% |
| SHARPE | 0.86 | 0.81 | 0.83 | 0.58 |
| WIN% | 68.7% | 66.2% | 52.6% | – |
| TRADES | 195 | 106 | 19 | – |
Very frequent rebalancing in weekly timeframe results in highest Sharpe (0.86) for lumber/gold strategy due to higher exposure to bonds but at higher cost of lower annualized return and not much improvement in maximum drawdown as compared to the other two strategies. A conservative choice may be momentum with 9.3% CAGR and lowest MDD at -19.4%. If someone is to surrender total return performance for the comfort of higher risk-adjusted returns, then the choice is probably momentum. Reducing transaction costs and rebalancing frequency is of paramount importance to many investors, traders but also hedge funds. Momentum has only 19 trades. Rotation has 106 but lumber/gold ratio 195 or about 84% more than rotation.
Conclusion
Selecting a commodity ratio as a metric for rebalancing, increases risk related to regime changes in the relationship of those commodities and the market. A simpler alternative that doesn’t have these issues is the best choice. I would go with rotation but momentum is also good provided there won’t be an extended multi-year sideways market in US stocks. Sideways markets can destroy momentum returns and even render these strategies highly unprofitable.
Superior risk-adjusted returns should be evaluated in the context of what simpler alternatives can offer. More importantly, financial journals and publications should start scrutinizing claims made by strategy developers that do not appear to factor in sufficient level of trading friction. Many experienced trading strategy developers know well that there are many hypothetical edges that vanish after the introduction of trading cost. An example is the overnight price action anomaly in SPY ETF.
Disclaimer: No part of the analysis in this blog constitutes a trade recommendation. The past performance of any trading system or methodology is not necessarily indicative of future results. Read the full disclaimer here.
Charting and backtesting program: Amibroker. Data provider: Norgate Data
If you found this article interesting, you may follow this blog via RSS or Email, or in Twitter
Price action Lab premium Content: By subscribing you have immediate access to hundreds of articles. Premium Insights subscribers have immediate access to more than a hundred articles, Premium Articles and Market Signals subscribers have immediate access to hundreds of articles that include the trader education section and All in One subscribers have access to all past premium content. Click here for more details.