I offer analysis in this blog motivated by a reply to a tweet I made yesterday regarding the essence of the 200-day moving average. I show that the choice of a 200-day moving average for the purpose of stock-bond allocation is sub-optimal. Furthermore, any reduction in drawdown levels can be attributed to the asset allocation rather than to some particular choice of moving average.
This is the tweet I made yesterday and a reply from Jake:
@mikeharrisNY allocate to stocks when above and bonds when below over longer periods, you get almost all return with 1/3 the volatility
— Jake (@EconomPic) June 30, 2015
Let us investigate Jake’s claim. Basically Jake suggested this strategy:
If price of SPY > 200-dma then sell TLT and buy SPY sell SPY if price of SPY < 200-dma and buy TLT.
I used initial capital of $100K, fully invested equity and $0.01/share commission. The backtest starts at the inception date of TLT, which is 07/30/2002. Below is the portfolio equity and underwater equity curve:
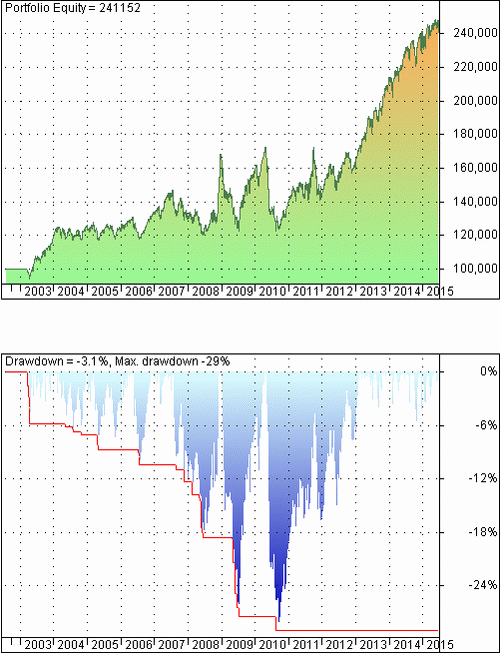
Equity and drawdown for allocation based on a 200-day moving average. Charts created with AmiBroker – advanced charting and technical analysis software. http://www.amibroker.com
Maximum drawdown is about half of what is realized by a buy and hold strategy in SPY. Obviously, risk is reduced because a -29% maximum drawdown is much better than a maximum drawdown of -56% for the buy and hold case. The buy and hold CAR in the tested period for SPY is 8.81% and CAR for the allocation strategy is 7.05%, actually not too bad considering the 50% reduction in maximum drawdown.
However, the objective of this blog is to show that the choice of the 200-day moving average is not special. To achieve that, I repeated the backtest for values of the moving average between 100 and 500 in increments of 20 days. Below are the results of the optimization:
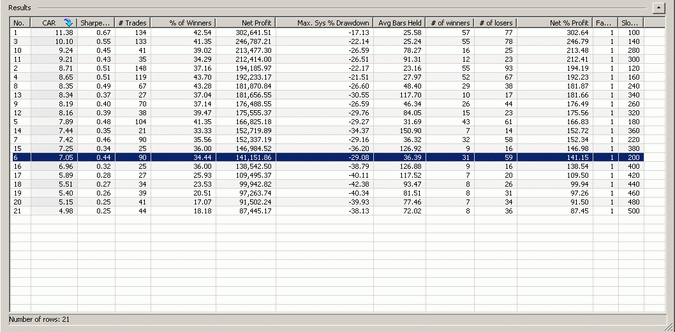
Charts created with AmiBroker – advanced charting and technical analysis software. http://www.amibroker.com
As it turns out the choice of a 200-day moving average is arbitrary and sub-optimal. A 100-day moving average results in the highest CAR of 11.38% at an even lower maximum drawdown of -17.13%. Below is the portfolio equity and underwater equity curve:
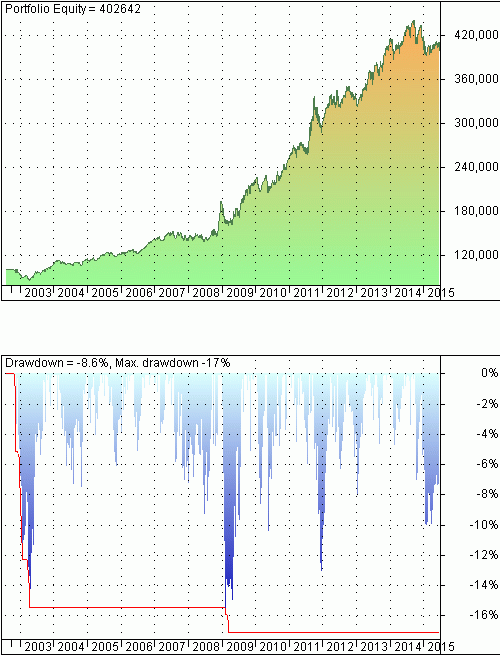
Equity and drawdown for allocation based on a 100-day moving average. Charts created with AmiBroker – advanced charting and technical analysis software. http://www.amibroker.com/
Therefore, I stand by my claim that the 200-day moving average was an invention of financial journalists that maybe later became a sort of (unsuccessful) self-fulfilling prophecy. In reality, the benefits of lower risk are inherent in the general allocation scheme and have little to do with the choice of moving average, except for values above 300 days where a large lag kicks in and drawdown levels increase.
Update:
@QuantStratTradR Done. 46-146 has the highest CAR. 16-140 has lowest max DD. 50-200 -29% DD at lower CAR.
— Michael Harris 📈 (@mikeharrisNY) July 1, 2015
You can subscribe here to notifications of new posts by email.
Charting program: Amibroker
Disclaimer
Detailed technical and quantitative analysis of Dow-30 stocks and popular ETFs can be found in our Weekly Premium Report.
© 2015 Michael Harris. All Rights Reserved. We grant a revocable permission to create a hyperlink to this blog subject to certain terms and conditions. Any unauthorized copy, reproduction, distribution, publication, display, modification, or transmission of any part of this blog is strictly prohibited without prior written permission.







Emlyn Flint
Hi Michael,
Poor performance under a single realisation is a necessary but not sufficient condition for a strategy being called 'sub-optimal'. Given the tests and results above, your point on the choice of MA PERHAPS being immaterial is valid (and very NB) but your conclusion on strategy (sub)optimality is a stretch. That requires more rigorous testing.
Assuming memory properties within the stock price process, there will always be an optimal TAA rule in the limit, even if they are are time-dependent. Assuming pure GBM with no memory, there will not.
Regards,
Emlyn
Michael Harris
Hello Emlyn,
As you also noted, my only objective in this blog was to show that
"However, the objective of this blog is to show that the choice of the 200-day moving average is not special."
I don't think I made any conclusions about strategy sub(optimality). If I did, please let me know. The blog did not assess the merits of the strategy.
"Assuming memory properties within the stock price process, there will always be an optimal TAA rule in the limit, even if they are are time-dependent"
Possible but this has to be proved rigorously and in my opinion, since performance is path-dependent, a general proof cannot exist. Also we have to define what TA rule stands for and correct for data-snooping.
"Assuming pure GBM with no memory, there will not."
Again, I'm not sure about that. GBM exhibits long trends. A suboptimal strategy under GBM is momentum investing. It's another issue whether it works but it is a good one and to this point it appears that it works.
Best regards,
Michael
Emlyn Flint
Thanks for the feedback Michael,
My first comment was more just of a facetious jab at your line: "I show that the choice of a 200-day moving average for the purpose of stock-bond allocation is sub-optimal." The 'is' got to me 🙂
On my comments on memory and type of stochastic process, I meant that if one limits the set of TA strategies to single-asset strategies that implicitly rely on auto-correlation then if one knows the underlying parameters of the process, one can design a strategy which *is* theoretically optimal (in expectation) but may only become practically optimal (in PnL) given enough time (and assuming we don't blow up before reaching that point!).
On the pure GBM process, surely TA will never be more or less optimal than anything else because the errors are assumed iid from an elliptical distribution and parameters are fixed ad infinitum? This is irrespective of the trend parameter value, which would obviously suggest a directional bias in any strategy.
Anyway, thank you for all the great articles. A voice of sanity and statistical rigour in the very noisy quantitative blogosphere.
Regards,
Michael Harris
Hi Emlyn,
"…if one knows the underlying parameters of the process, one can design a strategy which *is* theoretically optimal (in expectation) "
True but this does not guarantee minimum risk of ruin. Maybe a better optimization should involve maximization of a function of expectation and risk of ruin. However, solutions are sub-optimal to the degree that any practical solution may be as good: For example, low fixed fractional risk percent along with percentage stop-loss levels. Actually this is the practical/sub-optimal solution applied by my software, Price Action Lab. It designs a system and through the application of a small stop-loss it hopes that the average trade will converge to the positive expectation before the drawdown gets too large. Obviously, there is always a component of luck in anything we do, no matter how practical or sophisticated it is. If market conditions do not change dramatically when a system is first deployed and it manages to accumulate some equity, then it may survive through the hard times and beyond.
Michael
Emlyn Flint
Fair point, and well made.
Bill
Hello Michael,
I find systems with Price Action Lab (btw excellent program) that work well in both SPY and TLT. Is this another way of switching between bonds and stocks?
Thanks for the article. Bill.
Michael Harris
Hello Bill,
I would not consider that a traditional asset allocation method.
Raphael
Michael,
the really interesting task for me would be to figure out a way to make the MA periods adaptive. For example dependent upon realised volatility, etc.
Michael Harris
Hi Raphael,
In general this is a good idea. But in practice the risk of curve-fitting is high because adaptation involves more parameters and in many cases optimization. My opinion is that the simplest possible rules have the best chance of succeeding.
Here is one way of implementing adaptive moving averages:
Grant
I think all this really means is that in that particular period, the 100 day MA was better than the 200 day MA. Unfortunately, it doesn't tell us anything about which strategy will be best going forward.
Michael Harris
Exactly! That was one of the main points, i.e., there is nothing special about the 200-ma and a different ma will be optimal under different circumstances depending on the path taken.
Kelly Pinkham
Michael,
How did you understand that Riccardo's suggestion would operate — by dividing one's portfolio into 4 equal amounts and trading them separately per the 50/100/150/200 MA's? Thanks for any clarification you can provide.
Michael Harris
I think he meant scoring the performance using probably 11 month returns and switching to the model that scores best. However, I think is best to ask him is he is still around to maybe elaborate on that.
Riccardo Ronco
absolutely not! It is quite simple. The assumption is that we do not know which trend length is "ideal" so give up the holy grail with adaptive moving average unnecessary complications.
Consider 4 models where you give +1 or zero to these conditions:
Close > average close 50? yes +1, no zero
…
Close> average close 200 yes +1, no zero
so each day (or week if you use weekly data) you will have a score from 0 to 4 that you can normalize from o% to 100%
each day (week) you merely control this score and change the exposure accordingly.
Do that on a BASKET of multi-asset classes ETFs or sectors.
If you like, you can normalize volatility rather than equal weight.
But give up the idea of finding the best parameter: focus on finding a model that capture a characteristic of the market. If you use an algo to change time length of the average (or any other indicator) you assume that, for example, volatility is the factor to use. But why? What if volatility will become too low and your parameter will turn out to be extremely long. You are going to have a massive negative skewness like buy & hold. By making the system "adaptive" you have not made, IMHO, the model more robust: you have made the model a f() of something else.
Michael Harris
It's hard to say of this method works without any backtests.
Riccardo Ronco
then better to use 4 models and average them in a score. Say, use 50, 100, 150 and 200 day averages and get a score from 0% to 100%. This way the model is more robust.
On top of that rotating into bonds could be dangerous: I do not remember happening for the US market but the Italian market in 2011 saw a sell in both stocks and bonds and in that case you would have sold equities to buy collapsing bonds. So, I guess, you need a filter on bonds as well. Just in case.
Great article
Michael Harris
Hello Riccardo. I like your idea about averaging models in a score. Yes, it is possible that stocks and bonds get correlated. I think in US that has happened only during bull markets, such as in the 2000s uptrend. It is difficult to get correlation during bear markets because US bonds are still considered a safe heaven, at least for now. But in countries where there is a financial crisis and no reserve currency bonds and stocks can go down together. Your point is good. Thanks.
Riccardo Ronco
and with years of QE we have the genuine possibility of rates going higher impacting both stocks and bonds. The fact that has happened in Italy does not mean it will not happen in US, even if you have printing ability on your currency.
The score approach is the best way I have found to make a model robust in a simple way. What is crucial is to capture the trend one way or another. For bonds I suggest using a ratio like TLT vs SHY to know where to park cash when out of stocks.