There are software programs that allow combining technical indicators with entry and exit conditions to design trading strategies that fulfill desired performance criteria and risk/reward objectives. Due to data-mining bias, it is very difficult to differentiate the random strategies from those that may possess some intelligence in pairing their trades with market returns.
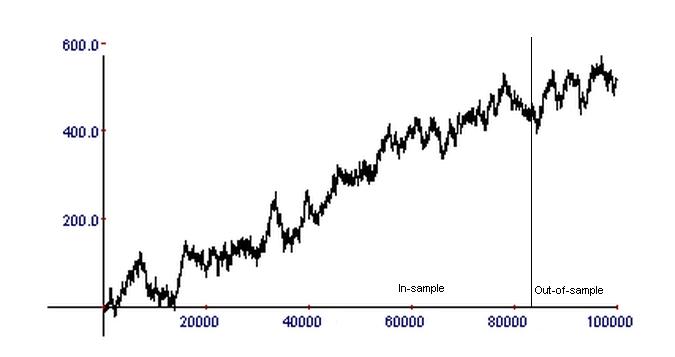
Suppose that you have such a program and you want to use it to develop a strategy for trading SPY ETF. After several iterations, manual or automatic, you get a relatively nice equity curve in the in-sample and the out-of-sample with a total of about 1000 trades (horizontal axis):
Before obtaining the above equity curve, many combinations of entry and exit methods were tried, usually hundreds or thousands, and in some cases, billions or even trillions. A large number of equity curves were generated that were not acceptable. You may think that this is a good equity curve, but you also suspect the strategy may be random due to data-mining bias arising from multiple comparisons. Below is another example where the developer thinks that by increasing the number of trades, randomness is minimized.
In this example, the number of trades was increased by two orders of magnitude to about 100,000, and both the in-sample and out-of-sample performances look acceptable. Does this mean that in this case, the strategy has a lower probability of being random?
The answer is, no. Both of the above equity curves were generated by tossing a coin with a payout equal to +1 for heads and -1 for tails. The second equity curve was generated after only a few simulations. Both curves are random. You can try the simulation yourself and see how successive random runs can, at some point, generate nice-looking equity curves by luck alone.
The correct logic here is that random processes can generate nice-looking equity curves, but how can we know if a nice-looking equity curve, which was selected from a group of other not-so-nice-looking curves, actually represents a random process and the underline algorithm has no intelligence? This inverse question is much more difficult to answer.
The coin-toss experiment illustrates that when one uses a process that generates many equity curves, some acceptable and some unacceptable, one may get fooled by randomness. Minimizing data-mining bias that arises from overfitting, data snooping, and selection bias is a complex and involved process that, for the most part, falls outside the capabilities of the average developer who lacks an in-depth understanding of these issues. The methods for analyzing strategies for the presence of bias are in many cases more important than the methods used to generate them and are considered an integral part of a trading edge.
Below are some suggestions for minimizing the probability of having found a random strategy:
(1) When selection from a group of alternative equity curves must be made, is the underlying process that generated the equity curve deterministic or does it involve randomness? If randomness is involved and each time the process runs, the strategy with the best equity curve is different, then the probability that it is a random strategy is very high. The justification for this is that a large number of edges can’t exist in a market, and, as a result, most of those strategies must be flukes.
(2) If you remove the exit logic of the strategy and apply a small profit target and stop-loss just outside the 1-bar volatility range, does the system remain profitable? (This test applies to short-term trading strategies.) If not, then the probability that the system possesses no intelligence in timing entries is high. This is because a large class of exits, such as trailing stops, overfit performance to the price series. If market conditions change in the future, the system will fail.
(3) Does the generated strategy involve indicators with parameters optimized to get the final equity curve through the maximization of some objective function(s)? If there are such parameters, then the data-mining bias increases with the number of parameters involved, making it extremely unlikely that the system possesses intelligence. Using more than one indicator will most likely lead to random strategies.
(4) Does the software used to generate strategies run only once to produce the final result in the in-sample or are multiple runs involved? If many runs are involved, the data-mining bias is large. This bias is the result of the dangerous practice of using data from the in-sample multiple times with many combinations of indicators and heuristic rules until an acceptable equity curve is obtained. Some of the strategies that generate good performance curves in the in-sample may also generate good equity performance in the out-of-sample just by chance alone. Limiting the number of hypotheses tested and the number of runs reduces data-mining bias.
(5) This is the most important consideration: If results of an out-of-sample test are used to start a fresh run or adjust the strategy parameters manually, then, in addition to possible over-fitting and selection bias, data-snooping bias is also introduced. In this case, validation of an out-of-sample beyond the first run is useless because the out-of-sample has become part of the in-sample. If an additional forward sample is used, then this reduces to the original in-sample/out-of-sample problem, and there is a high probability that the performance in the forward sample is due to chance.
More details and specific examples can be found in Chapter 6 of the book, Fooled By Technical Analysis.
You may follow this blog via RSS or Email, or in Twitter.
© 2012 – 2024 Michael Harris. All Rights Reserved. We grant a revocable permission to create a hyperlink to this blog subject to certain terms and conditions. Any unauthorized copy, reproduction, distribution, publication, display, modification, or transmission of any part of this blog is strictly prohibited without prior written permission.