In a recent blog I argued that the chances of finding a profitable trading algo via machine learning are for all practical purposes zero due to the large data-mining bias. One method of checking machine learning algorithms for the generation of spurious results is by testing them on random data.
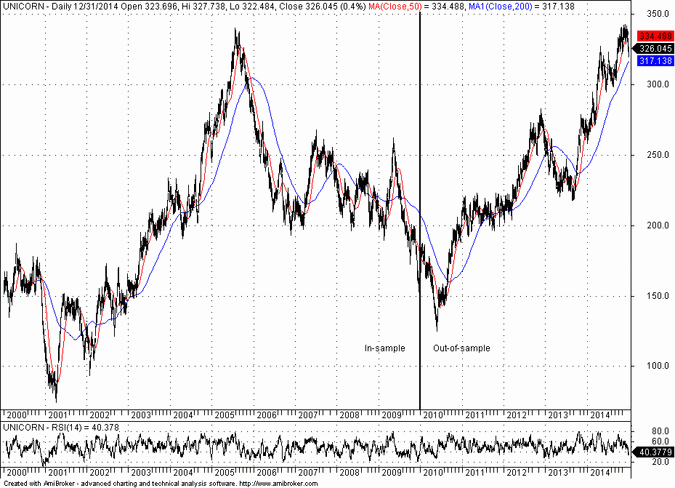
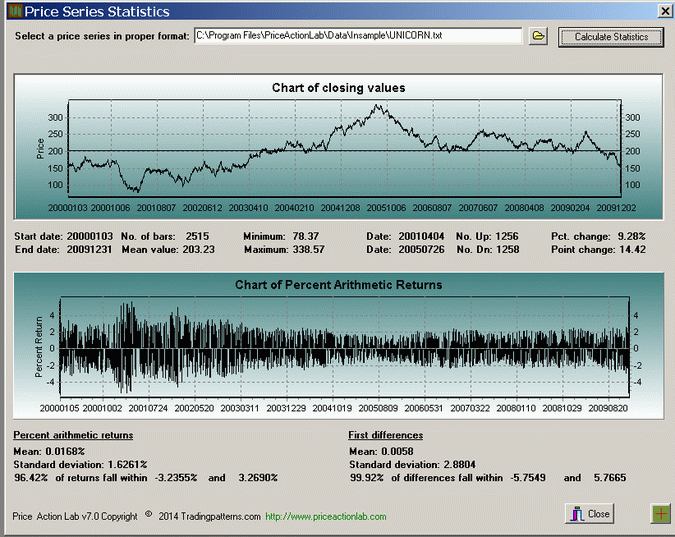
I generated random daily data for security UNICORN from 01/2000 to 12/2014. The first 2/3 of the random series will be used for in-sample machine learning and data-mining and the remaining 1/3 is reserved for out-of-sample cross-validation. Below is the chart of the UNICORN security:
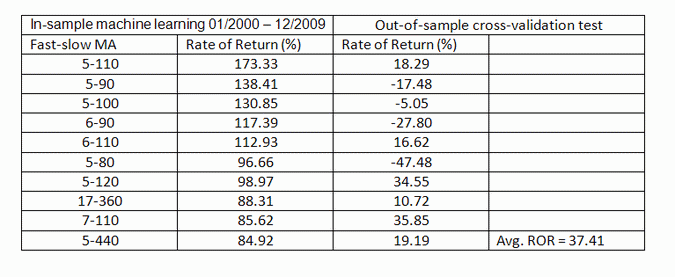
I used a machine leaning genetic algorithm with only a moving average crossover indicator as input to reduce data-mining bias. It is known that as the number of available indicators increases, data-mining bias also increases due to a larger space of multiple comparisons. I also used a simple metric to rank systems based on the rate of return on initial capital of 100K and with equity fully invested on each trade. The ten top performers in the in-sample with the corresponding values for the fast and slow moving are shown on the table below along with the out-of-sample results
As expected the best performer in the in-sample is not also the best in the out-of-sample. The best out-of-sample result is for a fast moving average of 7 periods and a slow moving average of 110 periods.
Obviously, selecting the top performer from an out-of-sample test is a mistake that apparently many users of machine learning algos do. The reason is that due to multiple comparisons it is highly likely that this is a spurious result. In this case it is because our data is random. We should not expect any system to perform well on random data. As a matter of fact, we should expect that the ROR of the system will be close to zero before commissions because this is what trading random data means. Apparently, some of the in-sample results perform well on the out-of-sample by luck. Just imagine what happens if the data is not random. In that case many more results perform well by luck alone. However, we will look at the ensemble of all ten systems, i.e. take the average of the returns in the out-of-sample. This comes out to 37.41% but it should be close to zero. Therefore, our machine learning algorithm generated systems that even perform well on random data.
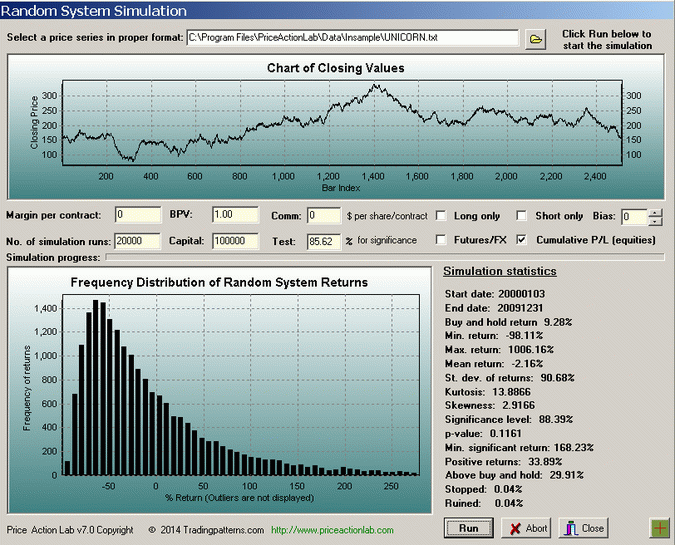
One should never pick the top performer from the out-of-sample. It is most likely a random result. Note that the in-sample performance of the top out-of-sample performer is not significant, as a randomization study shows based on a fair coin flip to generate 20K random trading systems:
For an in-sample return of 85.62% generated by the top out-of-sample performer, based on 20K random systems the p-value comes out to 0.1161. Therefore, given there is no evidence against the null hypothesis, this can be considered a spurious result even in the in-sample. The top performer in the in-sample is significant based on a minimum significant return of 168.23% but as it turns out the out-of-sample performance is not satisfactory.
Top performers in cross-validation tests are not always significant due to data-mining bias from multiple comparisons. It is better to consider an ensemble of top performers from the in-sample, I would recommend at least ten but as many as possible, and determine performance in the out-of-sample. If the data is random and the ensemble performance is positive, this could mean that the results are spurious to start with. In other words, the machine learning algorithm produces highly fitted results in the in-sample and some or even many of them survive in the out-of-sample. If the data is random, the ensemble performance should be flat in out-of-sample before commissions. This shows how easy it is to get fooled by machine learning algorithms.
Deterministic parameter-free data-mining
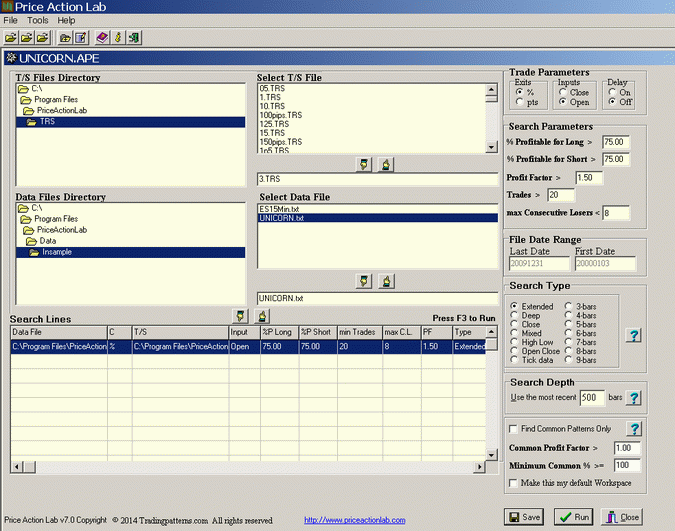
I used Price Action Lab to search for price patterns in the in-sample using the following workspace:
Each pattern in the in-sample must have at least 20 trades, 75% win rate, profit factor greater than 1.5 and no more than 7 consecutive losers (< 8). I used a profit target and stop-loss of 3% as determined by the following price series analysis in the in-sample:
Since 96.42% of all daily returns fall within -3.23% and 3.26% I chose 3% for the exits.
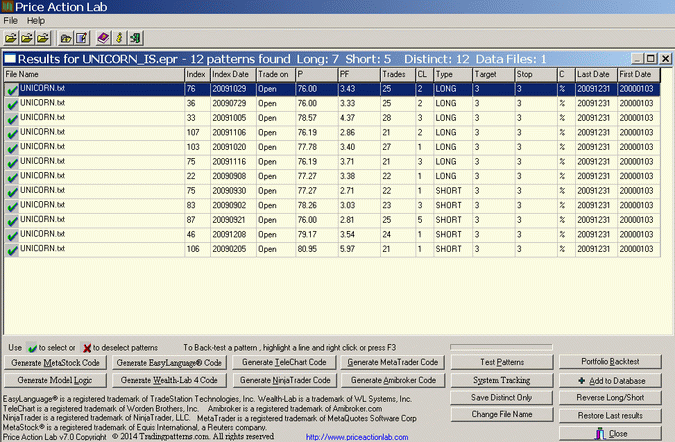
The results of the search are shown below:
Each line in the above results corresponds to a price pattern that satisfies the performance parameters specified by the user. Trade on is the entry point, in this case the Open of next bar. P is the success rate of the pattern, PF is the profit factor, Trades is the number of historical trades, CL is the maximum number of consecutive losers, Type is LONG for long patterns and SHORT for short patterns, Target is the profit target, Stop is the stop-loss and C indicates whether % or points for the exits, in this case it is %. Last Date and First Date are the last and first date in the historical data file.
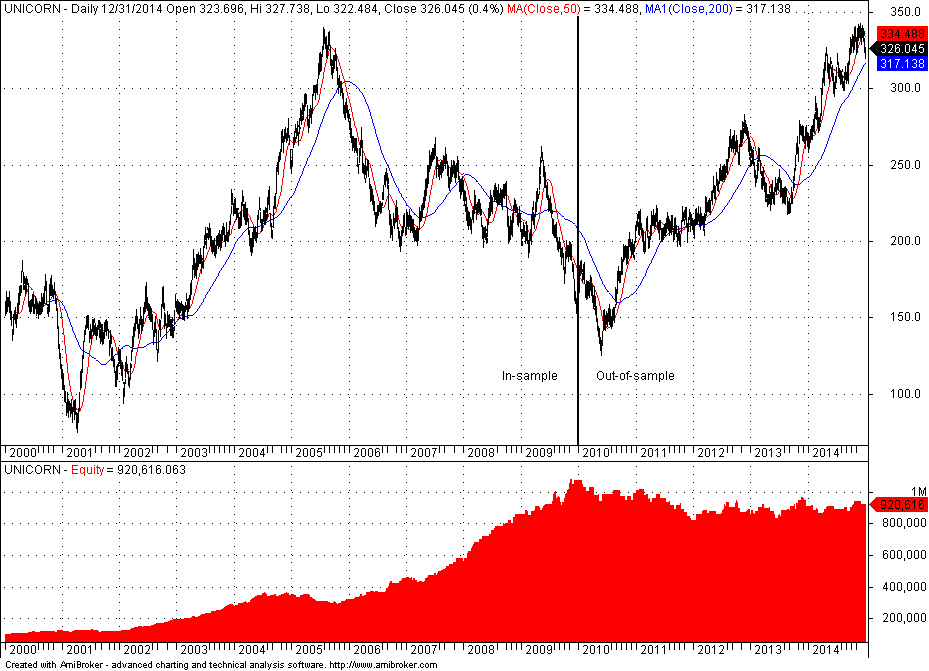
Twelve patterns were found in the in-sample of the random data that satisfied the performance parameters, seven long and 5 short. The question is: How do they perform in the out-of-sample? To answer this question I had the program generate Amibroker code for all patterns. The Boolean operator “OR” was used to combine the pattern code. Below is the equity curve of the backtest:
It may be seen that the equity line stays flat to slightly negative after the end of the in-sample. This is the expected behavior. In the in-sample twelve patterns survived but the ensemble fails in the out-of-sample because the data is random and the expectation should be close to zero. Note that there is nothing more to do here except for maybe trying different exits because there are no more metrics and indicators to use. There is no room for increasing the data-mining bias in favor of a positive but spurious result.
Using random data to test data-mining algos can provide important information about their integrity. Although there can be no conclusive test, this is one test to do before trying actual market data.
You can subscribe here to notifications of new posts by email.
Charting program: Amibroker
Disclaimer
© 2015 Michael Harris. All Rights Reserved. We grant a revocable permission to create a hyperlink to this blog subject to certain terms and conditions. Any unauthorized copy, reproduction, distribution, publication, display, modification, or transmission of any part of this blog is strictly prohibited without prior written permission.